タイトルのとおりです。セキスペを取りました。登録セキスペにも申請済みで、来月から正式に登録セキスペとなる見込みです。

ご無沙汰しております。IMAXおじさんです。

11.28〜12.1まで開催されていたAWS re:Invent 2023に参加してきました。これに行く前にAWSの資格を一つくらい取得しておきたいと思い立ち、AWS Solutions Architect - Associateを受験しました。 結果は合格(760/1000)でした。次はDeveloper Associateの取得を目指します。

お久しぶりです。IMAXおじさんです。

今日はこのサイトをさくらVPSからAWSに移行した話をします。現在はさくらVPSに戻しております。

元の構成(さくらVPS)に関して

元々はさくらVPSで小さめのサーバを借りてnginx + django + mysqlの構成でサイトを構成していました。詳細はこちらの記事に掲載しています。

この構成でやりたいことはだいたいできており、不満は全くなかったのですがお仕事でAWSを使い始めたこともあり、こちらに移行することにしました。

AWSでの構成に関して

個人サイトなのであまりお金がかかるのも困りものです。そこで、下の要求を満たすように構成を考えました。

• 月間予算20$ ~ 25$に収まるようにする
• さくらVPSで構築していたコンテナをそのままEC2に移行するのではなく、S3やALBなどを使って、なるべくAWSの機能性を活かした構成にする
• それぞれのサーバのログをS3に保管し、分析できるようにする

まだ全てを満たす構成にはできていませんが、現在は下のような形でデプロイをしています。

やりのこしていること

• ログの分析
• お部屋の気温分析アプリをIoT Core + IoT Analytics + Grafanaで実装

簡単な自作競プロジャッジサーバーを作った話をします。(競プロとは？：こちらを参照） デプロイしてから結構経つのに、詳細な構成に関して何も記事を書いていなかったので、ここらで文章に落とそうと思います。 サーバは一時期まで公開していましたが、Dockerで実行環境を隔離しているとはいえ任意のコードが実行できてしまうのは怖いので最近は公開していません。

1. ジャッジサーバの構成に関して

ジャッジサーバ内のコンポーネント間の構成とデータフローを示します。

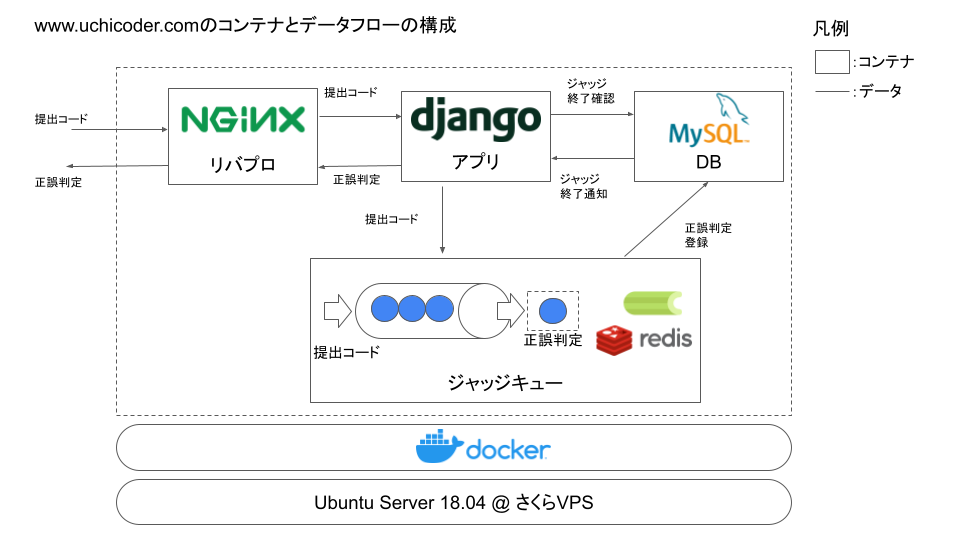
回答提出から正誤判定までのジャッジサーバ内での処理の流れ

1. 回答者からコードが提出されると、一旦Djangoがそれを受け取ります。
2. DjangoはこれをRedis+Celeryで実装された非同期処理ジャッジキューに突っ込みます。その後、ユーザに対しジャッジ処理中である旨を示します。
3. ジャッジキューは順に提出コードの正誤判定を行ない、判定終了したコードに対し完了フラグを立てます。
4. ジャッジ完了後、各コードの正誤判定の詳細をユーザに返します。

2. 難しかったところ

非同期処理の実装

コードを提出してから、ジャッジが完了するまでにある程度時間がかかります。 実行に時間がかかる場合やテストケースが多い場合は、POSTしてからページが表示されるまで何も表示されない状態になってしまいます。 また、実行時間があまりに長い場合はブラウザにリクエストタイムアウトと判定されてしまいま す。 そのため、今回は下記のようなフローで非同期処理を実装することにしました。

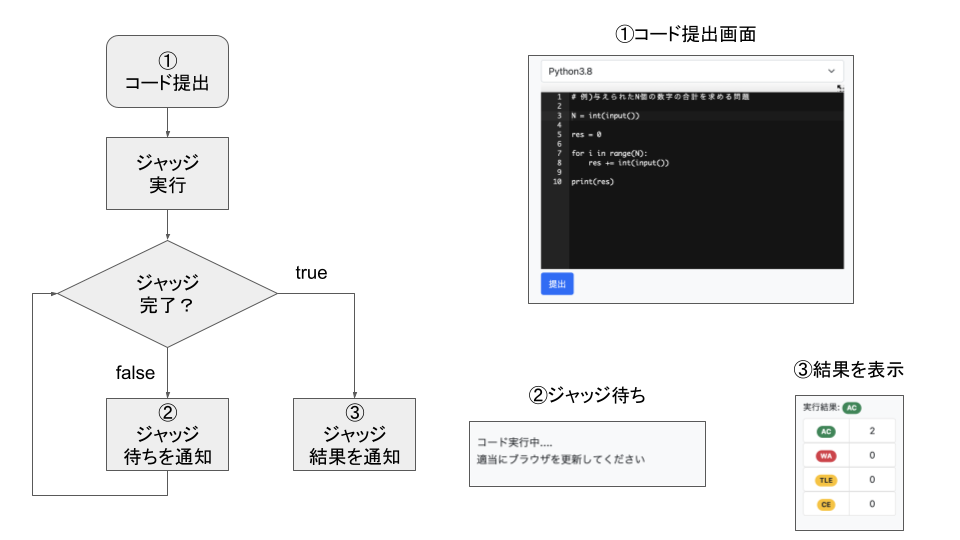
バックエンドではジャッジがcelery+redisで実装されたFIFOキューを保持し、提出されたコードに順次正誤判定を行なっています。 ジャッジ未完了の状態ではブラウザ更新を促し、ジャッジ完了の状態では結果を通知します。

TLEの検知

競技プログラミングにおいては、コードの実行時間が非常に重要です。多くの場合、2秒程度の実行時間内に問題を解けるコードを書く必要があります。 制限時間内に解けなかったコードにはTLE(Time Limit Exceeded)判定が与えられ、不正解扱いとなります。

最初は簡単なジャッジサーバができれば良い程度に考えていたので、コードの正解・不正解しか判定しないロジックを書いていました。 ところが、段々と完成度を追求したくなってくるもので、やはりTLEの判定がしたくなってきます。

色々実行時間を計測する術を検討しました。例えば、下記のようにコード実行前後で時刻を計測し、その差分を測るようなやり方です。

start = time.time()
ret = subprocess.run(cmd, shell=True, ...) #提出コードを実行
end = time.time()

timeTaken = end - start # 実行時間を計測

しかし、このやり方ではwhile True: passのような無限ループが発生した場合にTLE判定を出せなくなってしまいます。 一定時間以上実行している場合には途中で実行を打ち切るような動作が必要になるわけです。

最終的にはコードを実行しているsubprocessモジュールで実行時間を計測し、オーバーした場合にTLE判定を出すようにしました。 subprocessモジュールには、実行時間を制限するオプションtimeoutがあるため、ここに実行制限時間の秒数を渡せば上記の問題に対応しつつTLEを判定できます。

# subprocessモジュールによるコードの実行
try:
    ret = subprocess.run(
        cmd, timeout=2, shell=True, stdin=fin, #  timeoutに制限時間を指定
        stdout=subprocess.PIPE, stderr=subprocess.PIPE
    )
except (CalledProcessError, TimeoutExpired) as e:
    if TimeoutExpired:
        tle += 1  # 実行時間が超過した場合はTLE判定を出す
        continue

    elif CalledProcessError:
        ...

3 今後の予定

• フロントエンドをVue.jsで作り直す。
• ajaxによる非同期通信を実装し、ユーザがブラウザ更新をする必要をなくす
• 対応言語を増やす(現在Java, C++, Python3, PyPy3に対応)
• etc....

タイトルの通り、ソートアルゴリズムを真面目に実装します。 言語はPython、実装するソートアルゴリズムはクイックソート・ヒープソート・マージソートです。

ソートは基本的に標準ライブラリのsort関数に投げがちなので、内部がどうなっているかを気にすることがないかと思います。 今回は応用情報技術者試験の対策も兼ねて、真面目にソートを実装します。 なお、めんどくさいので昇順ソートしか実装しません()

参考文献

• 応用情報技術者試験合格教本(技術評論社)
• プログラミングコンテストのためのアルゴリズムとデータ構造(マイナビ出版)
• クイックソート
• ヒープソート
• マージソート(Qiita)
• マージソート

クイックソート

クイックソートは、分割統治の考え方でソートを行うアルゴリズムです。

下記のような配列を考えたとき、その配列に対してpivotと呼ばれる軸を設定し、そのpivot未満の配列とpivot以上の配列に分割していきます。 これを再帰的に繰り返すことで、整列済みの配列を得るアルゴリズムです。また、安定なソートではありません。

計算量

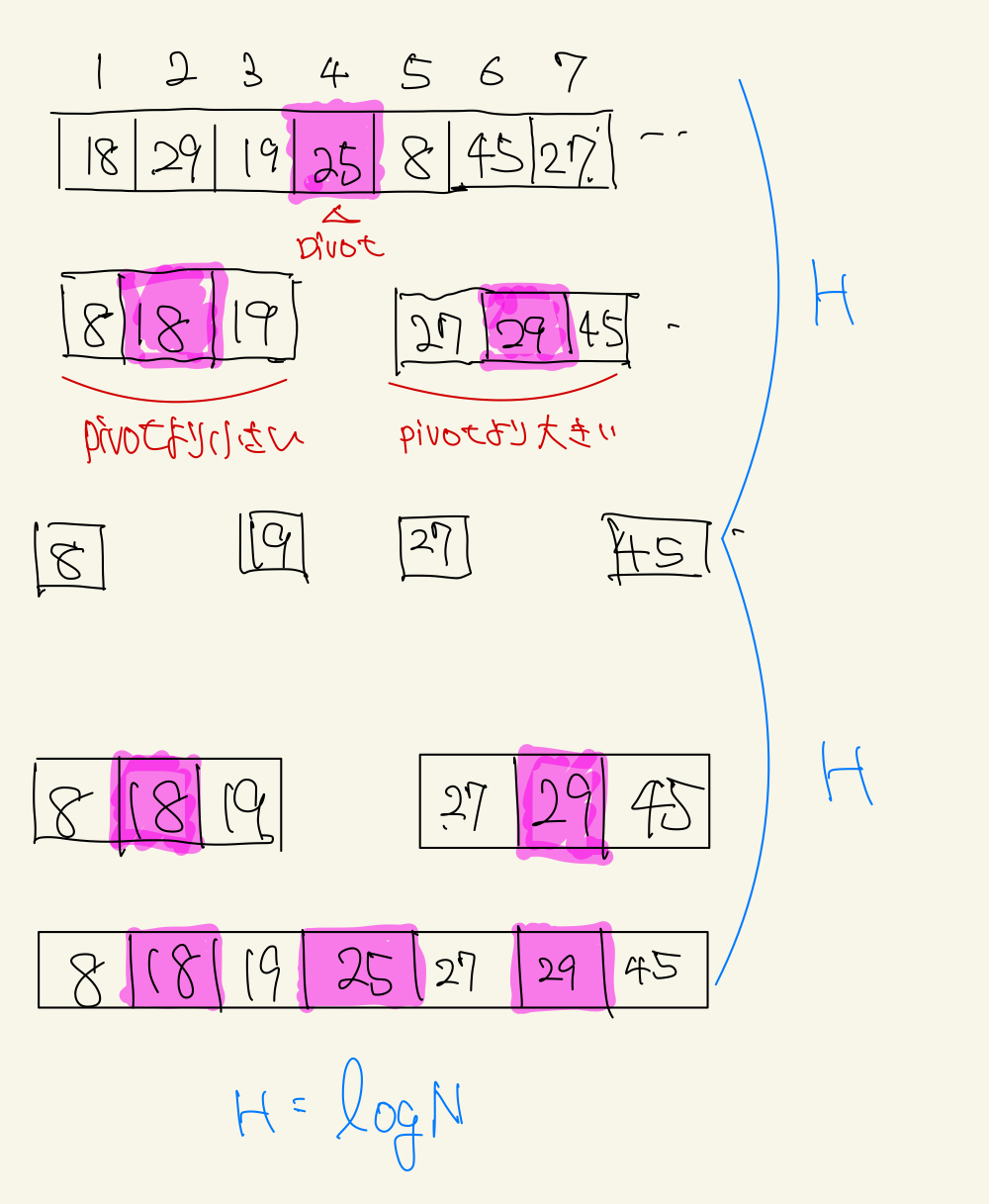
平均計算量は、O(NlogN)となります。 具体的な計算量の導出はこちらが参考になりました。

ざっくり言えば、適切にpivotを選んだ場合上記の画像で示す通りpivotによる分割と結合はそれぞれ回数H = logNで抑えることができます。 それぞれの高さに関して、N回比較が発生するので、計算量はO(NlogN)であるとわかります。

最悪計算量

ただし、予めソートされたデータに対して最大値/最小値をpivotとして取り続けた場合は最悪計算量がO(N^2)となります。

実装

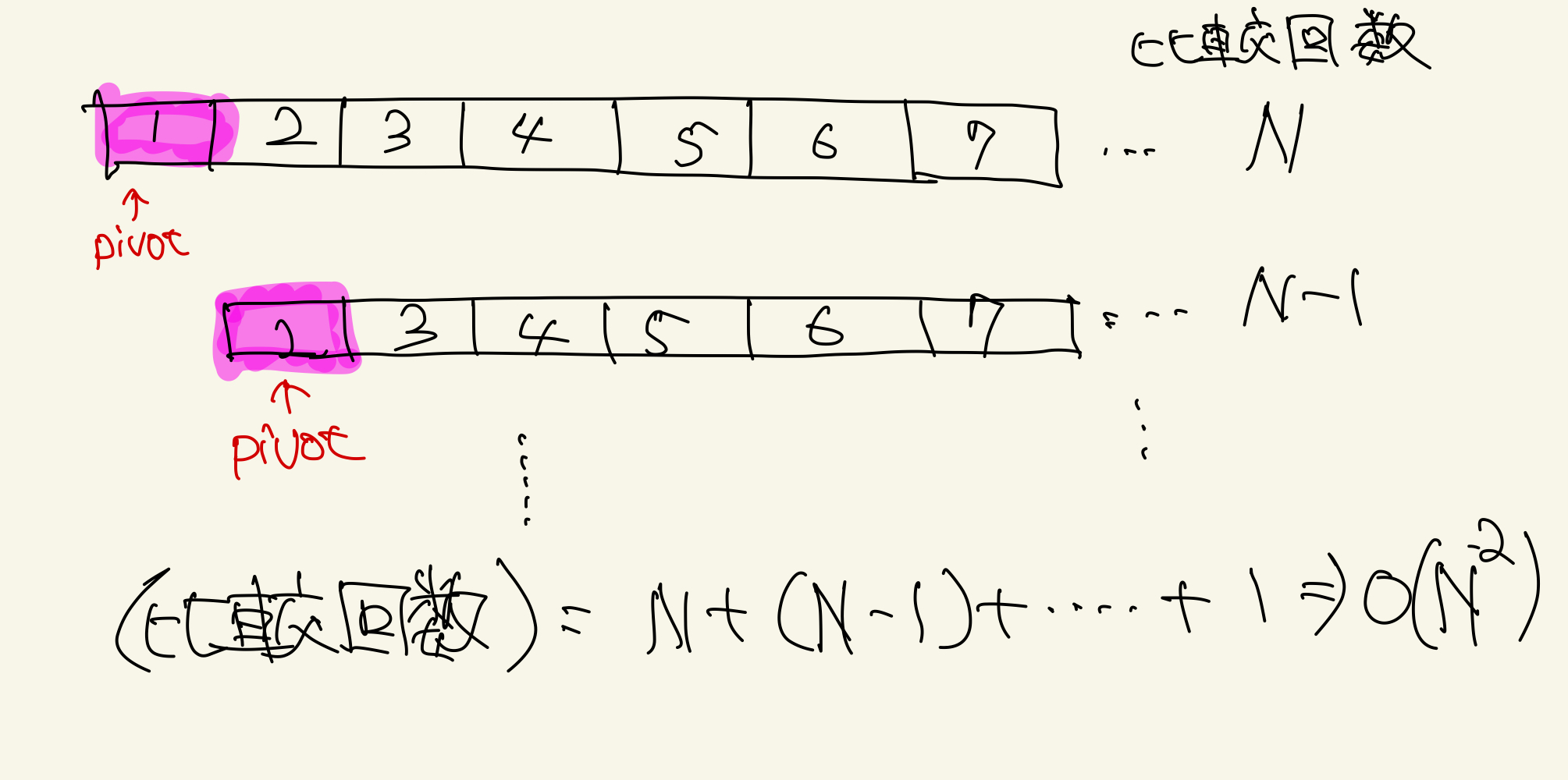
A = list(map(int, input().split()))
l = 0
r = len(A) - 1

def quick_sort(tgt):
    tgt_len = len(tgt)
    if len(tgt) <= 1:
        return tgt

    pivot = tgt[0]
    left = []
    right = []

    for i in range(1, tgt_len):
        if tgt[i] <= pivot:
            left.append(tgt[i])
        else:
            right.append(tgt[i])

    return quick_sort(left) + [pivot] + quick_sort(right)

res = quick_sort(A)
print(res)

ヒープソート

ヒープソートはヒープの再構成がO(logN)でできることを利用したソートアルゴリズムです。 ヒープの根が常に配列の最小値となっているので、ヒープの根をpop→ヒープを再構築...を繰り返し、popした順に配列を作ればO(NlogN)でソートできます。

ヒープに突っ込むため、安定なソートではないですが、常に計算量がO(NlogN)となります。

実装

ヒープを自力で実装し、ヒープからどんどんpopしていく方針を取ります。

class Heap:
    def __init__(self, arr:list):
        self.arr = []

        for item in arr:
            self.push(item)

    def push(self, x):
        self.arr.append(x)
        child = len(self.arr) - 1

        while child > 0:
            parent = (child - 1)//2

            if self.arr[parent] < x:
                break
            else:
                self.arr[child] = self.arr[parent]
                child = parent

        self.arr[child] = x

    def root(self):
        return self.arr[0] if self.arr else None


    def pop(self):
        if not self.arr:
            return None

        root = self.arr[0] 
        self.arr[0] = self.arr[-1]
        self.arr.pop()

        parent = 0
        smallest_index = parent
        heap_size = len(self.arr)

        while 2*parent+1 < heap_size:
            l = 2*parent+1  # 左の子
            r = l+1         # 右の子

            # 自分、左の子、右の子の中で、最小のものを選び取る
            if (r < heap_size) and (self.arr[parent] >= self.arr[r]):
                smallest_index = r

            if (l < heap_size) and (self.arr[smallest_index] > self.arr[l]):
                smallest_index = l

            # 自分が最小になった時点で、ヒープ化されたのでbreak
            if smallest_index == parent:
                break

            # 親と子を入れ替える
            self.arr[parent], self.arr[smallest_index] = self.arr[smallest_index], self.arr[parent]
            parent = smallest_index

        return root

def heap_sort(arr):
    heap = Heap(arr)
    N = len(arr)

    print(heap.arr)

    result = []
    for _ in range(N):
        result.append(heap.pop())
        print(heap.arr)

    return result

if __name__ == "__main__":
    sample = [1, 1, 2, -1, 100, 92]

    result = heap_sort(sample)

    print(result)  # -> [-1, 1, 1, 2, 92, 100]

マージソート

マージソートも、分割統治法の考え方を用いてソートを行うアルゴリズムです。 下記画像のように、まず要素が一つになるまで分割を繰り返します。

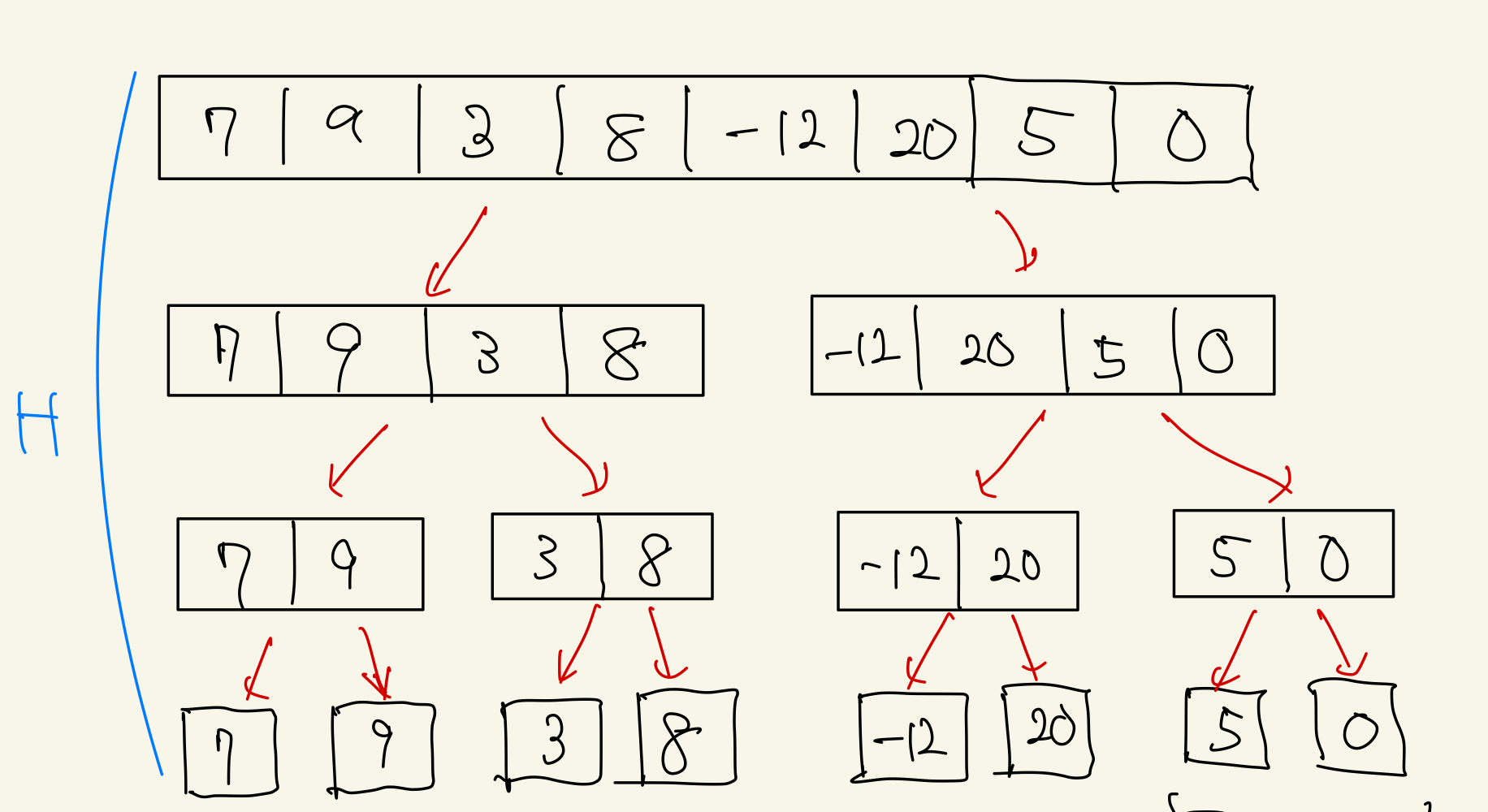
その後、分割した配列を２つずつマージしていきます。 このとき、分割した配列を結合する際に、昇順になるように入れていきます。各配列はソート済みであるので、それぞれ先頭のindexから順に比較していけば良いことになります。

計算量

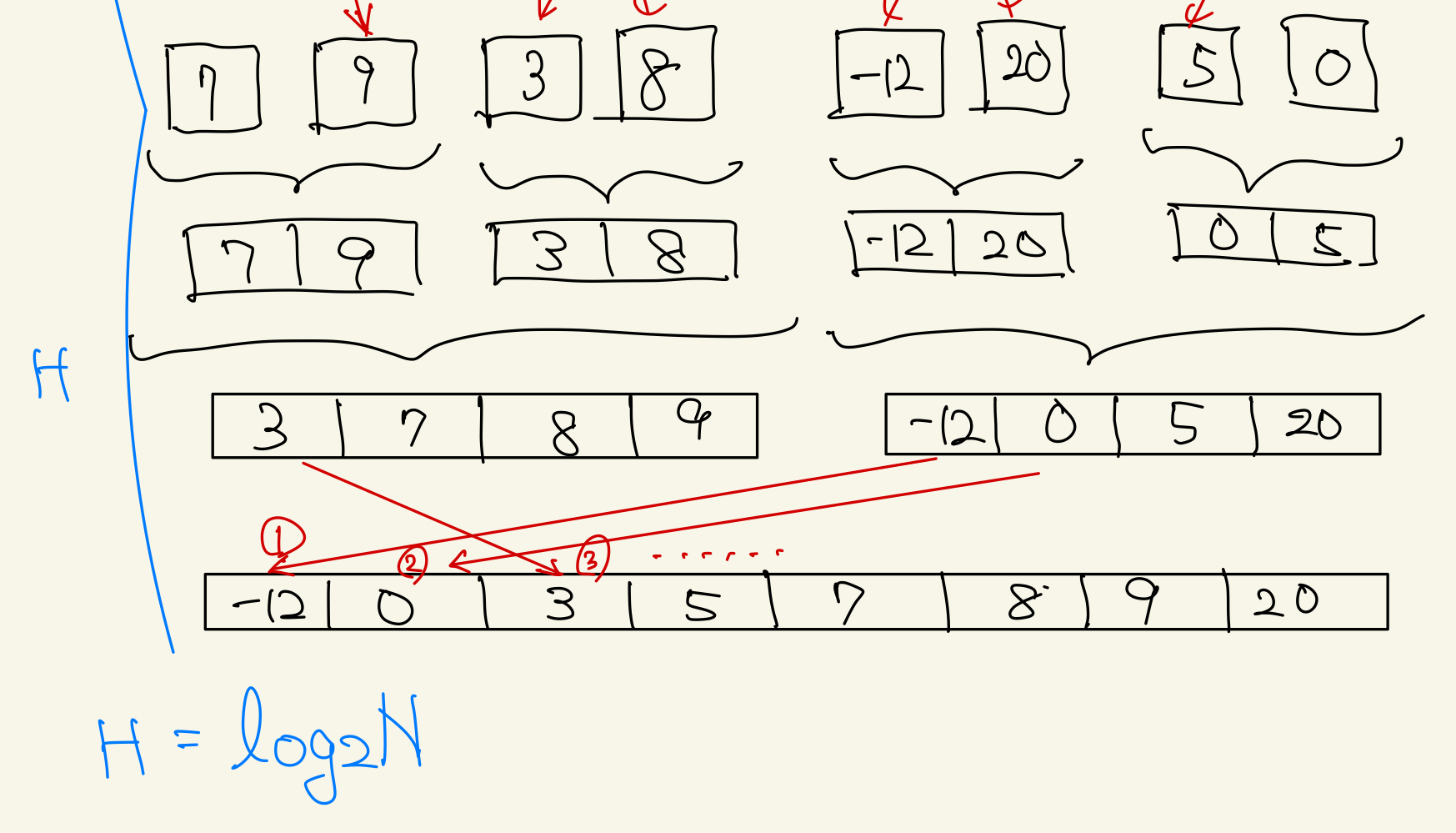
こちらの説明がとてもわかりやすいです。

上の図で示した通り、分割とマージのプロセスはそれぞれH = logNで抑えられます。 マージの際には、それぞれの分割のレイヤーでN回比較が走るので、結果的に計算量はO(2NlogN) = O(NlogN)となります。

実装

再帰的な実装を行います。（実は分割のところがO(N)かかっているのではないかという説があります）

def merge_sort(data):

    if len(data) <= 1: return data

    mid = len(data) // 2

    # 再帰的に分割していく
    left = merge_sort(data[:mid:])
    right = merge_sort(data[mid::])

    return merge(left, right)


def merge(left, right):
    result = []
    i, j = 0, 0

    # 配列の先頭が最小値になっているので、毎回比べながら追加していく
    while (i < len(left)) and (j < len(right)):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1

    # add the remainging part
    if i < len(left):
        result.extend(left[i:])

    if j < len(right):
        result.extend(right[j:])

    return result

if __name__ == "__main__":
    array = list(map(int, input().split()))

    res = merge_sort(array)

    print(res)